Angular Velocity Definition, Formula & Examples : Angular Velocity Formula implements to objects that move along a circular track.I will learn all about angular velocity with learn three types of the formulas we can use to step by step calculate this type of velocity.
You can also read my prev post like as a Mifflin St Jeor Calculator With Equation And Formula
What is angular velocity? – 5 BEST Angular Velocity Formula
Angular velocity implements to objects that move along a circular track. I will explore the definition of angular velocity as well as learn main 3 types of the different formulas I can use to calculate this type of velocity.
Moreover, I will explain the proper use of angular velocity calculator to determine the circular motion of an object. You will not only be able to calculate the angular velocity but also the angle of rotation, radial velocity of the object and linear velocity at any instant of time by using free angular speed calculator.
Angular velocity is less common than linear velocity, because it only implements to objects that are moving along a circular track. For instance, a racecar on a circular track, a roulette ball on a roulette wheel, or a ride, all have an angular velocity.
The angular velocity of an object is the object’s angular displacement as well as observe the time limit.
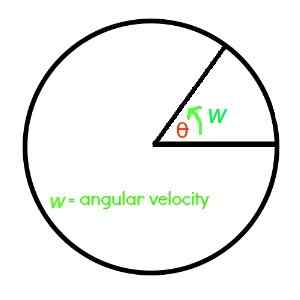
When an object is traveling along a circular track, the central angle corresponding to the object’s position on the circle is changing. The angular velocity, represented by w, is the rate of modification of this angle as well as observe the time limit.

For example Angular Velocity Formula, a ride could be rotating pi / 6 radians every minute. Therefore, the ride’s angular velocity would be pi / 6 radians per minute.
Linear Velocity
Before I can get to angular velocity, i will first review linear velocity. Linear velocity implementes to an object or particle that is moving in a straight line. It is the rate of modification of the object’s position as well as observe the time limit.
One of the most common examples of linear velocity is your speed when you are driving down the road. Your speedometer gives your speed, or rate, in miles per hour. This is the rate of modification of your position as well as observe the time limit, in other words, your speed is your linear velocity.
Linear velocity can be step by step calculated using the good formula vel_fml = sec_vel / time_scale, where vel_fml = linear velocity, sec_vel = distance traveled, and time_scale = time it takes to travel distance.
For simple example, if I drove 120 miles in 2 hours, then to calculate my linear velocity, I did plug sec_vel = 120 miles, as well as time_scale = 2 hours into my linear velocity formula to get vel_fml = 120 / 2 = 60 miles per hour.
Angular velocity formula
Angular Velocity is a evaluate of how quickly an object moves through an angle. It is the modification in angle of a moving object (evaluated in radians), divided by time. Angular velocity has a measure (a value) and a regulation.
Angular velocity = (ending angle) - (starting angle) / time = modification in position/time ω = (θf - θi) / time_scale ω = angular velocity θf = the ending angle θi = the starting angle time_scale = time Δθ = short form for 'the modification in angle'
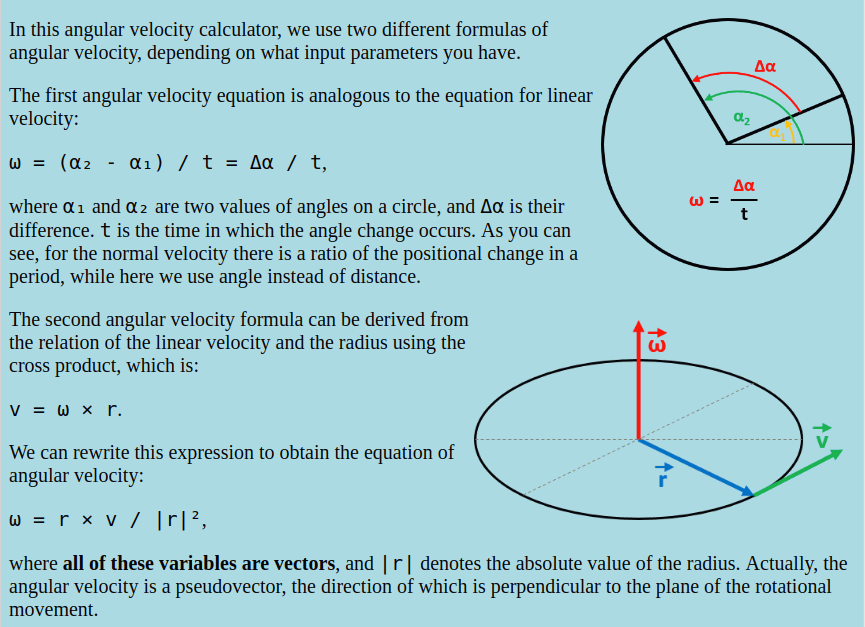
There are main 3 types of the formulas i can use to get step by step angular velocity.
Option 1
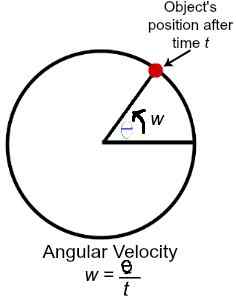
The first comes straight from the definition. Angular velocity is the rate of modification of the position angle of an object with observe the time limit, so w = theta / time_scale, where w = angular velocity, theta = position angle, and time_scale = time.
Angular velocity vs. angular frequency

Angular velocity units

Radians
I have one more thing to review before getting to angular velocity, and that is radians. When we deal as well as angular velocity, we use the radian evaluate of an angle, so it is important that we are familiar as well as radian evaluate.
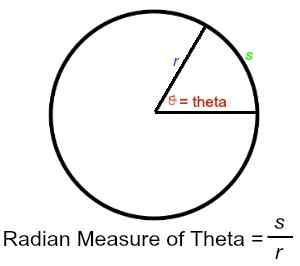
The technical definition of radian evaluate is the length of the arc specify by the angle, divided by the radius of the circle the angle is a part of, where specify means to be opposite of the angle and to extend from one point on the circle to the other, both marked off by the angle.
This tells us that an angle theta = s / r radians, where s = length of the arc corresponding to theta, and r = radius of the circle theta is a part of.
Since most of us are comfortable as well as the degree evaluatement of angles, it is convenient that we can easily convert degree evaluate to radian evaluate by multiplying the degree evaluate by pi / 180. For example, a 45 degree angle has a radian evaluate 45 (pi / 180), which is equal to pi / 4 radians.
How to find angular velocity of the Earth?

Angular Velocity vs. Linear Velocity
Building on the previous problem, imagine yourself on a very large merry-go-round, one as well as an unlikely radius of 10 kilometers (10,000 meters). This merry-go-round makes one complete revolution every 1 minute and 40 seconds, or every 100 seconds.
Simple conclusion of the difference between angular velocity, which is independent of the distance from axis of rotation, as well as linear circular velocity,
which is not, is that 2 people experiencing the same ω could be undergoing vastly different physical experienced. If you happen to be 1 meter from the center if this supposed, great merry-go-round, your angular linear (extraneous) angular velocity formula is:
(less than 3 inches) per second
Example: ωr = (2π radians/100 s)(1 m) = 0.0628 m/s, or 6.29 cm
yet if you are on the edge of this monster, your basic linear velocity is:
ωr = (2π radians/100 s)(10,000 m) = 628 m/s.
It’s more applicable 1,406 miles per hour, faster than a bullet. just moments!
Physical quantities dependent on the angular velocity

Conservation of angular momentum

Web Programming Tutorials Example with Demo
Read :
Summary
You can also read about AngularJS, ASP.NET, VueJs, PHP.
I hope you get an idea about angular velocity formula.
I would like to have feedback on my infinityknow.com blog.
Your valuable feedback, question, or comments about this article are always welcome.
If you enjoyed and liked this post, don’t forget to share.