where is the correct place to insert a javascript?

by
where is the correct place to insert a javascript

where is the correct place to insert a javascript? :

Today, We want to share with you where is the correct place to insert a javascript?.

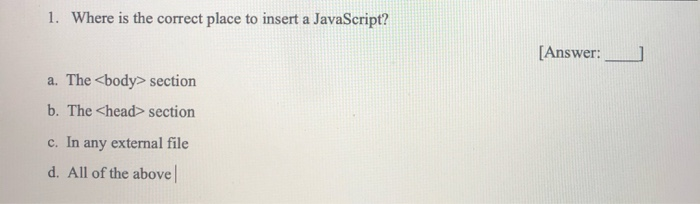
where is the correct place to insert a javascript?

In this post we will show you what is the correct way to write a javascript array??, hear for inside which html element do we put the javascript? we will give you demo and example for implement.

In this post, we will learn about Top 10 Advanced JavaScript Interview Questions Answers with an example.

the correct as well as best place to insert a JavaScript source code is The head part & The body part.

What are 3 places where JavaScript can be placed?

  • in between the two BODY tags
  • added a link to an external file
  • in between the two HEAD tags

calling javascript file in html

best place to include script in html layout

JavaScript in  or

what is the correct way to write a javascript
what is the correct way to write a javascript

You can added any number of scripts code in an HTML document. also It’s Scripts can be included in the 



 , or in the 




 part of an HTML page, or in both.


how to enter javascript in html?






where is the correct place to insert a javascript?

You can place any javascript code on script in the 




, or in the 




 part.


Where is the correct place to insert a JavaScript?


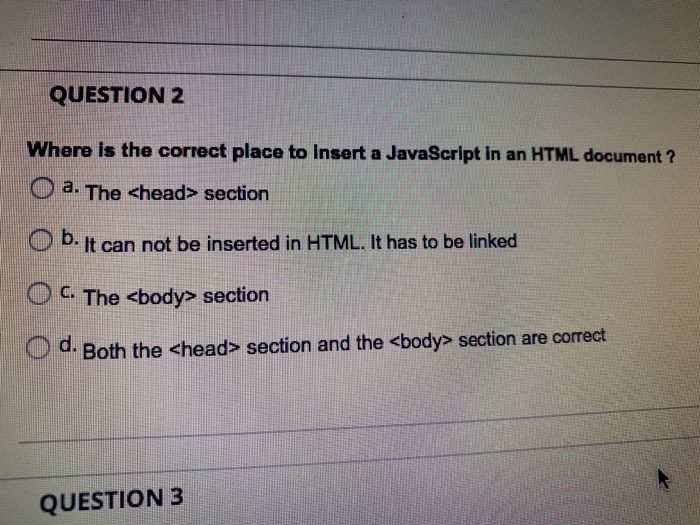
Where is the correct place to insert a JavaScript Mcq?


    

  • The head section
    • 

  •  The body section
    • 

  •  Both the head section and the body section are correct
    • 

  •  None of the above
    • 



Answer:


Both the  section and the  section are correct



JavaScript MCQ Quiz


what is the correct way to write a javascript array
what is the correct way to write a javascript array


Q : 1. In which element we put javascript?

Answer:  I put javascript in