In this post, we will learn about Trikonmiti Table, Trigonometry Table, Trigonometric table 0 to 360, etc.
Trikonmiti Table | Trigonometry table trick
Note: This trick will only work from 0° to 90° and not beyond that
- Sin θ: First of all write all the points from 0° to 90° in the line containing Sin as follows –
Now solve them, after that you will get the correct value of sin.
- Cos θ: Look at the trigonometry table at the top. The line containing Cos is the reverse order of the line containing Sin. That is, by writing the values of Sin in the order from 90° to 0°, you will get the values of Cos.
- Tan θ: Dividing the value of Sin by the value of Cos gives you the value of Tan.
- Cosec θ: It is the inverse of the value of Sin i.e. top number down and bottom number up
- Example: Sin 60° = √3/2 So writing it in reverse Cosec 60° = 2/√3
Similarly, the inverse of Cos is Sec and the inverse of Tan is Cot.
Trigonometric (Trikonmiti) Table 0 to 360
Here all the important formulas, ratios, values etc related to trigonometry table are described, which is essential for class 12th students and any exams. So below we have given the table of Trikonmiti Sarni i.e. Trigonometry.
Here are some steps to remember the above trigonometry table or tables.
First of all, we have to write the numbers 0, 1, 2, 3, and 4 for the angles 0°, 30°, 45°, 60°, and 90° respectively. And then we’ll divide each of the numbers 0, 1, 2, 3, and 4 by 4.
| 0/4 = 0 | 1/4 | 2/4 = 1/2 | 3/4 | 4/4 = 1 |
2. On dividing the numbers 0, 1, 2, 3, and 4 by 4, we get the numbers 0, 1/4, 1/2, 3/4, and 1. And now we’ll take the square root of these numbers.
| √0 = 0 | √1/4 = 1/2 | √1/2 = 1/√2 | √3/4 = √3/2 | √1 = 1 |
On taking the square root, the numbers obtained are 0, 1/2, 1/√2, √3/2,1 for sin ϴ.
3. By writing the values of 0, 1/2, 1/√2, √3/2, 1 for sin ϴ in the reverse order, we will get the values of cos ϴ.
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
4. Now we find the value for tan ϴ, for tan ϴ we have to divide the value of sin ϴ by the value of cos ϴ, because the formula for finding tan ϴ is: tan ϴ = sin ϴ/cos ϴ
| 0/1 = 0 | 1/2 ∕ √3/2 = 1/√3 | 1/√2 ∕ 1/√2 = 1 | √3/2 ∕ 1/2 = √3 | 1/0 = ∞ |
In this way, we get the values of tan ϴ as 0, 1/√3, 1, √3, ∞.
5. For the value of cosec ϴ, we have to take the reciprocal of the value of sin ϴ. This is the formula for cosec ϴ because cosec ϴ = 1/sin ϴ .
| 1/0 = ∞ | 1 ∕ 1/2 = 2 | 1 ∕ 1/√2 = √2 | 1 ∕ √3/2 = 2/√3 | 1/1 = 1 |
On taking the reciprocal of the values of sin ϴ, the numbers ∞, 2, √2, 2/√3, and 1 are the values of cosec ϴ.
6. If we write the values of cosec ϴ that we have taken out, ∞, 2, √2, 2/√3, and 1 in the reverse order, then we will get the values of sec ϴ.
1 |
2/√3 | √2 | 2 | ∞ |
7. The formula for cot ϴ is cot ϴ = 1/tan ϴ , so we’ll take the reciprocals of the values for tan ϴ to get the value of cot ϴ .
| 1/0 = ∞ | 1 ∕ 1/√3 = √3 | 1/1 = 1 | 1/√3=1/√3 | 0/1 = 0 |
So we get the values of cot ϴ as ∞, √3, 1, 1/√3 and 0.
In this way, you can calculate the values of sin ϴ, cos ϴ, tan ϴ, cosec ϴ, sec ϴ, cot ϴ up to 0°, 30°, 45°, 60° and 90° by using the above trigonometry tables. Value can be extracted.
Trigonometry Table Formula
| Degrees (°) | Sine (sin) | Cosine (cos) | Tangent (tan) | Cosecant (csc) | Secant (sec) | Cotangent (cot) |
|---|---|---|---|---|---|---|
| 0° | 0 | 1 | 0 | undefined | 1 | undefined |
| 30° | 1/2 | √3/2 | √3/3 | 2√3/3 | 2 | √3 |
| 45° | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | √3/2 | 1/2 | √3 | 2/√3 | 2 | 1/√3 |
| 90° | 1 | 0 | undefined | 1 | undefined | 0 |
| 120° | √3/2 | -1/2 | -√3 | -2/√3 | -2 | -1/√3 |
| 135° | √2/2 | -√2/2 | -1 | -√2 | -√2 | -1 |
| 150° | 1/2 | -√3/2 | -√3/3 | -2√3/3 | -2 | -√3 |
| 180° | 0 | -1 | 0 | undefined | -1 | undefined |
| 210° | -1/2 | -√3/2 | √3/3 | -2√3/3 | -2 | √3 |
| 225° | -√2/2 | -√2/2 | 1 | -√2 | -√2 | 1 |
| 240° | -√3/2 | -1/2 | √3 | -2/√3 | -2 | 1/√3 |
| 270° | -1 | 0 | undefined | -1 | undefined | 0 |
| 300° | -√3/2 | 1/2 | -√3 | 2/√3 | 2 | -1/√3 |
| 315° | -√2/2 | √2/2 | -1 | √2 | √2 | -1 |
| 330° | -1/2 | √3/2 | -√3/3 | 2√3/3 | 2 | √3 |
| 360° | 0 | 1 | 0 | undefined | 1 | undefined |
Trigonometry Ratio Table
| Trigonometry Ratio Table | ||||||||
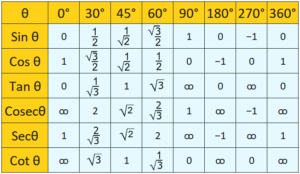
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (In Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
General Formulas of Trigonometry
- sinθ = perpendicular/hypotenuse = p / h
- cosθ = base/hypotenuse = b / h
- secθ = hypotenuse/base = h / b
- tanθ = perpendicular/base = p / b
- cotθ = base/perpendicular = b / p
- coescθ = hypotenuse/perpendicular = h / p
Relationships between Trigonometric Ratios
In trigonometry, there are several relationships between trigonometric ratios (sine, cosine, tangent, cotangent, secant, and cosecant) that can be used to simplify and solve problems. These relationships include:
- Cosecθ = 1 / sinθ
- Cosθ = 1 / Secθ
- Cosθ × Secθ = 1
- Cotθ = 1 / Tanθ
- Cotθ = Cosθ / sinθ
- Secθ = 1 / Cosθ
- Tanθ = 1 / Cotθ
- Tanθ = sinθ / Cosθ
- Tanθ × Cotθ = 1
- sinθ = 1 / Cosecθ
- sinθ × Cosecθ = 1
Important Trigonometry Formulas
There are several important formulas in trigonometry that are used to simplify expressions and solve problems. Some of the most important sources include:
- Cos θ / Cot θ = Sin θ
- Cosec θ / Sec θ = Cot θ
- Cot θ / Cosec θ = Cos θ
- Sec θ / Tan θ = Cosec θ
- Sin θ / Cos θ = Tan θ
- Tan θ / Sin θ = Sec θ
Trigonometry Table Trick
Friends, if you have any questions about Trigonometry Table, Trigonometric Table 0 to 360, Trigonometry Table, Trikonmiti Sarni, then you can ask by commenting, we will definitely help you. How did you like this post of ours, do tell us and share this post with your friends.